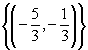Graphs
- To solve two equations graphically, we first draw the graphs of the two
lines. Their point of intersection is called the solution set.
Illustrative Examples
Example
Solve the equations y = 2x +1 and x +2y +3 = 0 graphically.
Alternatively, If P = {points (x, y), y = 2x +1} and Q={points (x, y), x+2y+3=0}, find P Q.
Q.
Solution
For equation y = 2x +1, we have the following:
Table of values
For equation x +2y +3 = 0, we get
2y = -x -3 or y = -x/2 -3/2
Table of values
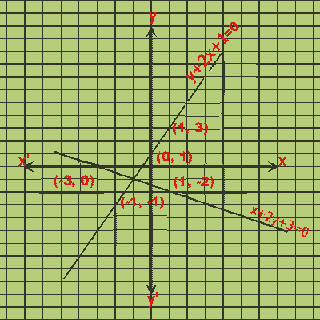
The graph is shown in above figure. We observe that these lines intersect at point (-1,-1).
Hence the solution set is P  Q = {(-1,-1)}.
Q = {(-1,-1)}.
We can verify that point (-1, -1) satisfies both equations:
2x +1 = 2 (-1) +1 = -1 = y; x +2y +3 = -1 +2 (-1) +3 = 0.
Exercise
- Draw the graphs of following lines:
(i) y = 2x
(ii) y = -3x
(iii) y = x/2
(iv) y = x +1
(v) y = x -1
(vi) y = 2x +1
(vii) y = x/2 -2.
- Draw the graphs of following lines:
(i) x = 0
(ii) y = 0
(iii) x = 1
(iv) x = -2
(v) y = 2
(vi) y = -3
- Draw the graphs of the following lines:
(i) x +y = 0
(ii) x -y = 0
(iii) 2x +3 = 0
(iv) 2x -3y +5 = 0
(v) 2x +2y -3 = 0
(vi) x/3 +y/3 = 1
(vii) x/2 -y/3 = 1
- Draw the graphs of following pairs of lines on the same
squared paper. Hence find their point of intersection.
(i) x +y -3 = 0 and x -y +7 = 0
(ii) x +3y -4 = 0 and 3x -y -2 = 0
(iii) 2x +y -3 = 0 and 3x +2y -4 = 0
- If P = {(x, y), 2x -y +3 = 0} and Q = {(x, y), x-2y+1=0}, find P
 Q.
Q.
- Draw the graphs of linear equations x = -2, x = 5, y = 0 and y = 4 on the
same squared paper. Hence find the area of the quadrilateral enclosed by these lines.
Answers
4. (i)(-2, 5)
(ii) (1, 1)
(iii) (2, -1)
5.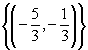
6. 28 square units
![]() Q.
Q.
![]() Q = {(-1,-1)}.
Q = {(-1,-1)}.