Heights and Distances
Exercise
- The angle of elevation of the top of a tower, from a point on the ground and at a distance of
150 m from its foot, is 30°. Find the height of the tower correct to one decimal place.
- From a point P on the level ground, the angle of elevation of the top of a tower is 30°. If the
tower is 100 m high, how far is P from the foot of tower?
- A kite is flying at a height of 75 meters from the level ground, attached to a string inclined at
60° to the horizontal. Find the length of the string to the nearest meter.
- If the length of a shadow cast by a pole be
 3 times
the length of the pole, find the angle of elevation of the sun.
3 times
the length of the pole, find the angle of elevation of the sun.
- A vertical tower is 20 m high. A man at some distance from the tower knows that the cosine
of the angle of elevation of the top of the tower is 0·53. How far is he standing from the foot
of the tower?
[Hint. If  is the angle of elevation, then cos
is the angle of elevation, then cos
 = ·53
=>
= ·53
=>  = 58°]
= 58°]
- (a) From a boat 300 meters away from a vertical cliff, the angles of elevation of the top and
the foot of a vertical concrete pillar at the edge of the cliff are
55° 40' and 54°20' respectively. Find the height of the pillar correct to the nearest meter.
(b) From a man M, the angle of elevation of the top of a tree is 44°. What is the angle of
elevation from the man of a bird perched half way up the tree?
- The upper part of a tree broken by wind, falls to the ground without being detached. The top
of the broken part touches the ground at an angle of 38° 30' at a point 6 m from the foot of
the tree. Calculate
(i) the height at which the tree is broken.
(ii) the original height of the tree correct to two decimal places.
- The angle of elevation of the top of a tower from a point A (on the ground) is 30°. On
walking 50 m towards the tower, the angle of elevation is found to be 60°. Calculate
(i) the height of the tower (correct to one decimal place).
(ii) the distance of the tower from A.
- From the top of a church spire 96 m high the angles of depression of two vehicles on a road,
at the same level as the base of the spire and on the same side of it are x° and y°, where tan
x° = 1/4 and tan y° = 1/7. Calculate the distance between the vehicles.
- The shadow of a vertical tower on level ground increases by 10 m, when the altitude of the
sun changes from 45° to 30°. Find the height of the tower correct to one decimal place.
- From a light house the angles of depression of two ships on opposite sides of the light house
were observed to be 30° and 45°. If the height of the light house is 90
meters and the line joining the two ships passes through the foot of the light house, find the distance between two
ships. Give your answer correct to 2 decimal places.
- From the top of a cliff 150 m high, the angles of depression of two boats are 60° and 30°.
Find the distance between the boats, if the boats are
(i) on the same side of cliff.
(ii) on the opposite sides of the cliff.
- Two pillars of equal height stand on either side of a roadway which is 120 m wide. At a
point in the road between pillars, the elevations of the pillars are 60° and 30°. Find the
height of the pillars and the position of the point.
- A girl, 1·6 m tall, is 20 m away from a tower and observes that the angle of elevation of the
top of the tower is 60°. Find the height of the tower.
- A man 2 m tall is 50 m away from a building 40 m high. What is the angle of elevation of the
top of the building from his eye?
- A man 1·8 m high stands at a distance 3·6 m from a lamp post and casts shadow of 5·4 m
on the ground. Find the height of lamp post.
- From the top of a building AB, 60 meters high, the angles of depression of the top and the bottom of
a vertical lamp post CD are observed to be 30° and 60° respectively. Find
(i) the horizontal distance between AB and CD.
(ii) the height of the lamp post CD.
- From the deck of a ship, the elevation of the top of a cliff is
 ° and from the top of a mast 50 m above the deck, the elevation is
° and from the top of a mast 50 m above the deck, the elevation is
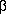 °. If tan
°. If tan
 ° = 1·2 and tan
° = 1·2 and tan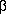 ° = 0·7, find the
height of the cliff above the deck.
° = 0·7, find the
height of the cliff above the deck.
- From the top of a building 20 m high, the angle of elevation of the top of a monument is 45°
and the angle of depression of its foot is 15°. Find the height of the monument.
- The angle of elevation of the top of an unfinished tower at a point distant 120 m from its
base is 45°. How much higher must the tower be raised so that its angle of elevation at the
same point may be 60°?
- The angle of elevation of a cloud from a point 200 meters above a lake is 30° and the angle of depression of its reflection
in the lake is 60°. Find the height of the cloud.
Answers
1. 86·6 meters
2. 173·2 m
3. 86·6 m
4. 30°
5. 12·5 m
6. (a) 21 m (b) 25° 46'
7. (i) 4·77 m (ii) 12·44 m
8. (i) 43·3 m (ii) 75 m
9. 288 m
10. 13·7 m
11. 245·88 m
12. (i) 173·2 m (ii) 346·4 m
13. 51·96 m; 30 m from the pillar whose angle of elevation is 60°
14. 36·24 m
15. 37° 14'
16. 3 m
17. (i) 34·64 m (ii) 40 m
18. 120 m
19. 94·65 m
20. 87·84 m
21. 400 m