Locus
- The locus of a point is the path traced out by the moving point under given geometrical
condition (or conditions). Alternatively, the locus is the set of all those points which satisfy
the given geometrical condition (or conditions).
- The locus of a point, which is equidistant from two fixed points, is the perpendicular
bisector of the straight line joining the two fixed points.
- The locus of a point, which is equidistant from two intersecting straight lines, consists of a
pair of straight lines which bisect the angles between the two given lines.
Exercise
- Draw and describe the locus in each of the following cases:
(i) The locus of points at a distance 2 cm from a fixed line.
(ii) The locus of points (in a plane) at a constant distance 2 cm from a fixed point in the plane.
(iii) The locus of points (in space) at a constant distance 2 cm from a fixed point.
(iv) The locus of centers of all circles passing through two fixed points.
(v) The locus of a point in the rhombus ABCD which is equidistant from the sides AB and AD.
(vi) The locus of a point in the rhombus which is equidistant from the points A and C.
(vii) The locus of center of a circle of varying radius and touching two arms of
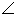 ABC.
ABC.
(viii) The locus of center of a circle of varying radius and touching a fixed circle, center
O, at a fixed point A on it.
(ix) The locus of center of a circle of radius 2 cm and touching a fixed circle of radius 3
cm with center O.
- A, B and C are three collinear points.
(i) Construct the locus of point equidistant from A and B.
(ii) Construct the locus of point equidistant from B and C.
(iii) Is it possible to locate a point equidistant from A, B and C.
- Take PQ = 6 cm. Construct
(i) the locus of points equidistant from P and Q.
(ii) the locus of points 5 cm from P.
Mark the two points which lie on both loci and measure the distance between them.
- In a triangle ABC, the right bisectors of AB and BC meet at P.
(i) Assign the special name to the point P.
(ii) Prove that PA = PB = PC.
(iii) If 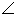 ABC = 90°, find the exact location of the point P with respect to the side AC.
ABC = 90°, find the exact location of the point P with respect to the side AC.
- Construct a triangle PQR with PQ = 5 cm, QR = 4 cm and RP = 3·6 cm. Find by
construction a point P which is equidistant from the three vertices P, Q and R.
- Construct a triangle ABC in which BC = 3·8 cm, CA = 4 cm and AB = 5·1 cm. Find by
construction a point P which is equidistant from BC and AB, and also equidistant from B and C.
- Construct a triangle ABC, in which AC = BC = 5 cm and AB = 6 cm. Locate the points
equidistant from AB, AC and at a distance 2 cm from BC. Measure the distance
between the two points obtained.
- Construct a triangle ABC, in which AC = BC = 5 cm and AB = 6 cm. Locate the points
equidistant from B, C and at a distance 2 cm from A. Measure the distance between the
two points obtained.
- Construct
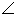 ABC = 75°. Mark a point P equidistant from AB and BC such that its
distance from another line DE is 2·3 cm.
ABC = 75°. Mark a point P equidistant from AB and BC such that its
distance from another line DE is 2·3 cm.
- Draw two intersecting straight lines to include an angle of 135°. Also locate points which
are equidistant from these lines and also 1·8 cm away from their point of intersection.
How many such points exist?
- AB and CD are two intersecting st. lines. Locate points which are at distances 2·5 cm
and 1·8 cm from AB and CD respectively. How many such points are there?
- Without using set square or protractor, construct the quadrilateral ABCD in which
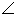 BAD = 45°, AD = AB = 6 cm, BC = 3·6 cm and CD = 5 cm.
BAD = 45°, AD = AB = 6 cm, BC = 3·6 cm and CD = 5 cm.
(i) Measure 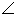 BCD.
BCD.
(ii) Locate the point P on BD which is equidistant from BC and CD.
- Without using set square or protractor, construct rhombus ABCD with sides of length 4
cm and diagonal AC of length 5 cm. Measure
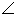 ABC. Find the point P on AD such that
PB = PC. Measure the length AP.
ABC. Find the point P on AD such that
PB = PC. Measure the length AP.
- ABCD is a rhombus with side 4 cm and
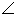 ABC = 120°. Construct the locus of points
inside the rhombus
ABC = 120°. Construct the locus of points
inside the rhombus
(i) equidistant from A and C.
(ii) equidistant from B and D.
(iii) equidistant from A and B.
- Draw a line segment AB of length 6 cm, M is mid point of AB. Construct
(i) the locus of points 3 cm from AB
(ii) the locus of points 5 cm from M.
Mark two points P and Q on the same side of AB satisfying the above loci. Measure the distance between P and Q.
- AB is a fixed line. Draw and describe the locus of the center of a circle of radius 2·5 cm
and touching the line AB.
- If the diagonals of a quadrilateral bisect each other, prove that the quadrilateral is a rhombus.
- Using ruler and compasses only, construct a quadrilateral ABCD in which AB = 6 cm,
BC = 5 cm,
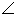 B = 60°, AD = 5 cm and D is equidistant from AB
and BC. Measure CD.
B = 60°, AD = 5 cm and D is equidistant from AB
and BC. Measure CD.
- Use ruler and compasses only for this question. Draw a circle of radius 4 cm and mark
two chords AB and AC of the circle of length 6 cm and 5 cm respectively.
(i) Construct the locus of points, inside the circle, that are
equidistant from A and C. Prove your construction.
(ii) Construct the locus of points, inside the circle, that are equidistant from AB and AC.
- Use ruler and compasses only for the following question:
Construct triangle BCP, where CB = 5 cm, BP = 4 cm, 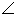 PBC = 45°. Complete the
rectangle ABCD such that
PBC = 45°. Complete the
rectangle ABCD such that
(i) P is equidistant from AB and BC, and
(ii) P is equidistant from C and D.
Measure and write down the length of AB.
Answers
1. (i) A pair of straight lines parallel to the given line.
(ii) A circle with fixed point as center and radius 2 cm.
(iii) A sphere with fixed point as center and radius 2 cm.
(iv) Perpendicular bisector of the line segment joining given points.
(v) Diagonal AC of the rhombus ABCD.
(vi) Diagonal BD of the rhombus ABCD.
(vii) The bisector of 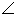 ABC.
ABC.
(viii) The straight line passing through O and A.
(ix) Concentric circle of radius 1 cm if circles touch internally; and concentric
circle of
radius 5 cm if circles touch externally.
2. (iii) No
3. 8 cm
4. (i) circumcenter
(iii) Mid-point of AC
7. 4·1 cm (app.)
8. 3·4 cm (app.)
10. Four
11. Four
12. (i) 65°.
13. 78°; 1·2 cm
14. (i) Diagonal BD
(ii) diagonal AC
(iii) right bisector of AB
15. (i) Pair of straight lines parallel to AB and at distance 3 units on either side of AB
(ii) Circle with center M and radius 5 cm; 8 cm
16. Pair of straight lines parallel to AB and at distance 2·5 cm on either side of AB
18. 5·25 cm approximately
19. (i) The diameter of the circle right bisecting AC
(ii) The segment of the circle bisecting 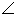 BAC.
BAC.
20. 5·5 cm (app.)