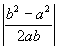Angle between two Lines
The angle between two non-vertical and non-perpendicular lines
- Let l1 and l2 be the two non-vertical and non-perpendicular lines with
slopes m1 and m2 respectively.
Let
 1
and
1
and  2 be their inclinations,
then m1 = tan
2 be their inclinations,
then m1 = tan  1
and m2 = tan
1
and m2 = tan  2.
There are two angles
2.
There are two angles  and
and  -
-  between the lines l1 and l2, given by
between the lines l1 and l2, given by
tan  = ±
(m1-m2)(1+m1m2)
= ±
(m1-m2)(1+m1m2)

Illustrative Examples
Example
Find the angle between the lines joining the points
(-1,2), (3,-5) and (-2,3), (5,0).
Solution
Here, m1 = slope of the line joining (-1,2) and (3,-5)
= (-5-2)/(3+1) = -7/4 and
m2 = slope of the line joining (-2,3) and (5,0)
= (0-3)/(5+2) = -3/7
Let  be the acute angle between the given lines, then
be the acute angle between the given lines, then
tan  =
=  .
.
=
Hence the acute angle  between the lines is given by
between the lines is given by
tan  = 37/49
= 37/49
Exercise
- Find the angle between the following pairs of lines:
(i) 3 x -7 y +5 = 0 and 7 x +3 y -11 = 0
(ii) 3 x +y -7 = 0 and x +2 y +9 = 0
(iii) y = (2 - 3) x +9 and y = (2 +
3) x +9 and y = (2 +
 3) x +1
3) x +1
(iv) 2 x -y +3 = 0 and x +y -2 = 0
[Hint. (iv) It will be found that acute angle  is given by tan
is given by tan  = 3
= 3
which gives  as 71° 34', by using tables of natural tangents]
as 71° 34', by using tables of natural tangents]
- Find the angle between the lines joining the points (0,0), (2,3) and (2,-2), (3,5).
- If A(-2,1), B(2,3) and C(-2,-4) are three points, find the angle between the lines AB and BC.
- Find the angles between the lines x +1 = 0 and
 3 x +y -3 = 0.
3 x +y -3 = 0.
- Find the angle between the lines which make intercepts on the axes a,-b and b,-a respectively.
- Find the measures of the angles of the triangle whose sides lie along the lines
x +y -5 = 0, x -y +1 = 0 and y -1 = 0.
- Find the equations of the two straight lines passing through the point (4,5) which make an
acute angle of 45° with the line 2 x-y +7 = 0.
- Find the equations of the two straight lines passing through the point (1,-1) and inclined at
an angle of 45° to the line 2 x -5 y +7 = 0.
- A vertex of an equilateral triangle is (2,3) and the equation of the opposite side is
x +y +2 = 0. Find the equations of the other two sides.
- One diagonal of a square lies along the line 8 x -15 y = 0 and one vertex of the square is
at (1,2). Find the equations of the sides of the square passing through this vertex.
- If (1,2) and (3,8) are a pair of opposite vertices of a square, find the equations of the sides and the diagonals of the square.
Answers
1.(i) 90° (ii) 45° (iii) 60° (iv) 71° 34'
2. 25° 34'
3. 33° 42'
4. 30°
5. The acute angle  is given by tan
is given by tan  =
=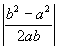
6. 45°, 45°, 90°
7. 3 x +y -17 = 0, x -3 y +11 = 0
8. 7 x -3 y -10 = 0, 3 x +7 y +4 = 0
9. (2 + 3) x -y -1 -2 = 0,
(2 -
3) x -y -1 -2 = 0,
(2 - 3) x -y -1 +2 = 0
3) x -y -1 +2 = 0
10. 23 x -7y -9 = 0, 7x +23 y -53 = 0.
11. Sides are 2 x +y -4 = 0, x -2 y +3 = 0,
2 x +y -14 = 0, x -2 y +13 = 0 and
diagonals are 3 x -y -1 = 0, x +3 y -17 = 0


![]() be the acute angle between the given lines, then
be the acute angle between the given lines, then![]() =
=  .
.
![]() between the lines is given by
between the lines is given by![]() = 37/49
= 37/49