Families of Circles
A collection of circles is called a family or a system of circles.
Let S and S' be two intersecting (or touching) circles, then S +k S'
= 0, k 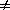 -1, represents a family of
circles through their points (or point) of intersection.
-1, represents a family of
circles through their points (or point) of intersection.
Remarks
- If k = -1, then the equation S +kS' = 0 reduces to S -S' = 0 which
represents the common chord in case of intersecting circles or common tangent
in case of touching circles.
- The equation S +kS = 0 represents all members of the family except the
member S'. If we need the member S', then take the equation of the family as S' +kS = 0.
Illustrative Examples
Example
Find the equation of the family of circles passing through the points A(0,4) and B(0,-4).
Solution
Let the equation of the desired family of circles be
x² +y² +2gx +2fy +c = 0 ...(i)
As all these circles pass through the points A(0,4) and B(0,-4), we get
0 +16 +0 +8f +c = 0 => 8f +c +16 = 0
...(ii),
0 +16 +0 -8f +c = 0 => -8f +c +16 = 0 ...(iii)
On solving (ii) and (iii), we get f = 0, c = -16.
Substituting these values in (i), we get
x² +y² +2gx -16 =0 ...(iv)
Note that for every real value of g,
g² +f² -c = g² +16 > 0, therefore, (iv) represents a circle.
Hence the equation x² +y² +2gx -16 = 0 for different real values of g
represents the desired family of circles. It is one-parameter family of
circles where g is the parameter.
Example
Find the equation of the circle which passes through the points of
inter-section of x² +y² -4 = 0 and x² +y² -2x -4y +4 = 0 and touches the line
x +2 y = 0.
Solution
The equations of the given intersecting circles are
S = x² +y² -4 = 0, and
S' = x² +y² -2 x -4y +4 = 0
The equation of the common chord of these circles is
S -S' = 0 => l = 2 x +4 +4 y -8 = 0
The equation of the family of circles passing through the intersection of the
given circles is
x² +y² -4 +k (2x +4 +4y -8) = 0 ...(i)
Its center is (-k,-2k) and
radius =  [k² +4k² +4 +8k] =
[k² +4k² +4 +8k] =
 [5k² +8k +4].
[5k² +8k +4].
For the particular member of the family which touch the line x +2y = 0, we have
|-k +2 (-2k)|/  [1² +2²] =
[1² +2²] =
 [5k² +8k +4]
[5k² +8k +4]
=> 5|k|/ 5 =
5 =
 [5k² +8k +4]
[5k² +8k +4]
=> 5 k² = 5 k²+8 k +4
=> 8 k +4 = 0 => k = -1/2
Substituting this value of k in (i), the equation of the required circle is
x² +y² -4 - (1/2)(2x +4y -8) = 0 i.e. x² + y² -x -2y = 0.
Exercise
- Find the equation of the family of circles passing through the origin.
- Find the equation of the family of circles passing through the origin and the point (0,1).
- Find the equation of the family of circles passing through the points A(5,0) and B(-5,0).
- Find the equation of the family of circles with radius 3 and whose centers lie on the x-axis.
- Find the equation of the family of concentric circles with center as
(-4,2). Also find a member of the family which touches the line x -y = 3.
- Show that the equation of the family of circles which touch both the
co-ordinate axes can be put into the form x² +y² ±2rx ±2ry +r² = 0,
where r is radius.
[Hint. Let ( ,
,
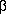 ) be center of the family. Since it touches both the axes
) be center of the family. Since it touches both the axes
i.e. y = 0 and x = 0, so | | = |
| = |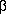 |
r =>
|
r =>  = ±r,
= ±r,
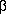 = ±r.]
= ±r.]
- Find the equation of the circle which passes through the origin and the
points of intersection of the circles x² +y² +2x +2y -2 = 0 and x² +y² +4x
-8y +4 = 0.
- Find the equation of the circle through the points of intersection of the
circles x² +y² +2x +3y -7 = 0 and x² +y² +3x -2y -1 = 0 and through the point (1,2).
- Find the equation of the circle which passes through the point (1,-1) and
through the points of intersection of the circles x² +y² +2x -2y -23 = 0 and
3x² +3y² +12x -4y -9 = 0.
- Find the equation of the circle passing through the point (2,3) and
through the points of intersection of the circle x² +y² +3x -4y +5 = 0 and the line x -y +2 = 0.
- Find the equation of the circle through the intersection of the circles
x² +y² -8x -2y +7 = 0 and x² +y² -4x +10y +8 = 0 and having its center on the x-axis.
Answers
1. x² +y² +2 gx +2 +2fy = 0, where g, f are any real numbers
2. x² +y² +2gx -y = 0, where g is any real number
3. x² +y² +2fy -25 = 0, where f is any real number
4. (x -h)² +y² = 9, where h is any real number
5. x² +y² +8x -4y +20 -r² = 0, where r is radius;
2(x² +y²) +16x -8y -41 = 0
7. 3(x² +y²) +8x -4y = 0
8. x² +y² +4x -7y +5 = 0
9. 32(x² +y²) +115x -47y -226 = 0
10. x² +y² -9x +8y -19 = 0
11. 6(x² +y²) -44x +43 = 0
![]() -1, represents a family of
circles through their points (or point) of intersection.
-1, represents a family of
circles through their points (or point) of intersection.![]() [k² +4k² +4 +8k] =
[k² +4k² +4 +8k] =
![]() [5k² +8k +4].
[5k² +8k +4].![]() [1² +2²] =
[1² +2²] =
![]() [5k² +8k +4]
[5k² +8k +4]![]() 5 =
5 =
![]() [5k² +8k +4]
[5k² +8k +4]