Equation of a Circle in different forms
A circle is the locus of a point which moves in a plane so that it remains
at a constant distance from a fixed point. The fixed point is called the
center and the constant distance is called radius. Radius is always positive.
Standard (or simplest) form
The equation of a circle with O(0,0) as center and r (>0) as radius is
x² +y² = r²
Central form
The equation of a circle with C(h,k) as center and r (>0) as radius is given by
(x -h)² +(y -k)² = r²
Diameter form
Let A(x1,y1) and B(x2,y2) be
the extremities of a diameter of the circle.
Then the equation of the circle is
(x -x1)(x -x2) + (y -y1)(y -y2) = 0
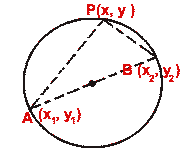
Illustrative Examples
Example
Find the equation of a circle whose center is (3,-2) and which passes
through the intersection of the lines 5x +7y = 3 and 2x -3y = 7.
Solution
Given lines are
5x +7y -3 = 0 ...(i), and
2x -3y -7 = 0 ...(ii)
Solving (i) and (ii) simultaneously, we get x = 2, y = -1.
So the point of intersection, say P, of the given lines is (2,-1).
Since the center of the circle is C(3,-2) and it passes through the point P(2,-1),
radius = |CP| =  [(2 -3)² +(-1 +2)²] =
[(2 -3)² +(-1 +2)²] =
 [1 +1] =
[1 +1] =  2
2
Hence the equation of the circle is
(x -3)² +(y +2)² = ( 2)²
(central form)
2)²
(central form)
or x² +y² -6x +4y +11 = 0.
Example
Find the equation of a circle which touches
- the y-axis at origin and whose radius is 3 units
- both the co-ordinate axes and the line x = 3.
Solution
- There are two circles satisfying given conditions. As the circles touch
y-axis at the origin, their centers lie on x-axis. Since radius is 3 units,
centers of the circles are (3, 0) and (-3, 0) and hence the equations of the circles are
(x ±3)² +(y -0)² = 3² or x² +y² ±6x = 0
-
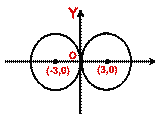
There are two circles satisfying the given conditions. From above figure,
clearly, the centers of these circles are and (3/2,3/2) and (3/2, -3/2)
radius of each circle is 3/2. So the required equation is
x² +y² -3x ±3y + (9/4) = 0
or 4x² +4y² -12x ±12y +9 = 0
Exercise
- Find the equation of a circle whose
(i) center is at the origin and the radius is 5 units.
(ii) center is (-1, 2) and radius is  5 units.
5 units.
- Determine the equation of a circle whose center is (8, -6) and which
passes through the point (5, -2).
- Prove that the points (7, -9) and (11, 3) lie on a circle with center at
the origin. Also find its equation.
- Find the equation of the circle whose
(i) center is (a, b) and passes through origin.
(ii) center is (2, -3) and passes through the intersection of the lines 3x -2y -1 = 0 and 4x +y -27 = 0.
- Find the equation of a circle whose center is the point of intersection
of the lines 2x +y = 4 and x -y = 5 and passes through the origin.
- Find the equation of a circle whose two diameters lie along the lines 2x
-3y +12 = 0 and x +4y + 12 = 0 and x +4y -5 = 0 and has area 154 square units.
- Find the equation of the circle whose center lies on the negative
direction of y-axis at a distance 3 units from origin and whose radius is 4 units.
- Find the equations of the circles of radius 5 whose centers lie on the
x-axis and pass through the point (2,3).
- Find the equation of the circle
(i) whose center is (0, -4) and which touches the x-axis.
(ii) whose center is (3, 4) and touches the y-axis.
- Find the equations of circles which touch both the axes and
(i) has radius 3 units
(ii) touch the line x = 2a.
- Find the equations of circles which pass through two points on x-axis at
distances of 4 units from the origin and whose radius is 5 units.
- Find the equations of circles
(i) which touch the x-axis on the positive direction at a distance 5 units
from the origin and has radius 6 units.
(ii) passing through the origin, radius 17 and ordinate of the center is -15.
(iii) which touch both the axes and pass through the point (2, 1).
- Find the equations of circles which touch the y-axis at a distance of 4
units from the origin and cut off an intercept of 6 units along the positive
direction of x-axis.
- Find the equations to the circles touching axis of y at the point (0, 3)
and making an intercept of 8 units on x-axis.
- Find the equations to the circles which touch the x-axis at a distance of
4 units from the origin and cut off an intercept of 6 from the y-axis.
Answers
1. (i) x² +y² = 25 (ii) x² +y² -2x +4y = 0
2. x² +y² -16x + 12y +75 = 0
3. x² +y² -130 = 0
4. (i) x² +y² -2ax -2by = 0
(ii) x² +y² -4x +6y -96 = 0
5. x² +y² -6x +4y = 0.
6. x² +y² +6x -4y -36 = 0
7. x² +y² +6y -7 = 0.
8. x² +y² -12x +11 = 0, x² +y² +4x -21 = 0
9. (i) x² +y² +8y = 0 (ii) x² +y² -6x -8y +16 = 0
10. (i) x² +y² ±6x ±6y +9 = 0
(ii) x² +y² -2ax ±2ay +a² = 0
11. x² +y² ±6y -16 = 0
12. (i) x² +y² -10x ±12y +25 = 0
(ii) x² +y² ±6x +30y = 0
(iii) x² +y² -2x -2y +1 = 0, x² +y² -10x -10y +25 = 0
13. x² +y² -10x ±8y +16 = 0
14. x² +y² ±10x -6y +9 = 0
15. x² +y² ±8x ±10y +16 = 0
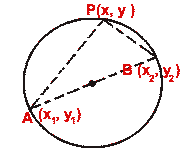
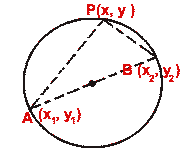
![]() [(2 -3)² +(-1 +2)²] =
[(2 -3)² +(-1 +2)²] =
![]() [1 +1] =
[1 +1] = ![]() 2
2![]() 2)²
(central form)
2)²
(central form)