A = P
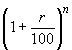 where A is the final amount, P is the principal, r is the rate of interest
compounded yearly and n is the number of years.
where A is the final amount, P is the principal, r is the rate of interest
compounded yearly and n is the number of years.C.I. = A -P =

Interest: It is the additional money besides the original money paid by the borrower to the money lender in lieu of the money used.
Principal: The money borrowed (or the money lent) is called principal.
Amount: The sum of the principal and the interest is called amount.
Thus, amount = principal +interest.
Rate: It is the interest paid on Rs 100 for a specified period.
Time: It is the time for which the money is borrowed.
Simple Interest: It is the interest calculated on the original money (principal) for any given time and rate.
Formula: Simple Interest = (Principal x Rate x time)/100
Compound interest (abbreviated C.I.) can be easily calculated by the
following formula:
A = P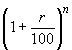 where A is the final amount, P is the principal, r is the rate of interest
compounded yearly and n is the number of years.
where A is the final amount, P is the principal, r is the rate of interest
compounded yearly and n is the number of years.
C.I. = A -P = 
Remark.
Interest may be converted into principal annually, semiannually, quarterly,
monthly etc. The number of times interest is converted into principal in a
year is called the frequency of conversion, and the period of time between two
conversions is called the conversion period or interest period. Thus "rate of
5%" means a rate of 5% compounded annually; 12% compounded semi-annually means
that each interest period of 6 months earns an interest of 6%. Thus the rate
of interest per interest period is
r = (annual rate of interest) / (frequency of conversion)
and the number of interest periods is
n = (given number of years) x (frequency of conversion).
In solving problems on compound interest, remember the following:
1. A = P 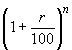 and C.I. =
and C.I. = 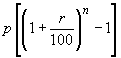
where A is the final amount, P is the principal, r is the rate of interest
compounded yearly (or every interest period) and n is the number of years (or
terms of the interest period).
2. When the interest rates for the successive fixed periods are r1
%, r2 %, r3 %, ..., then the final amount A is given by
A =
![]()
3. S.I. (simple interest) and C.I. are equal for the first year (or the first term of the interest period) on the same sum and at the same rate.
4. C.I. of 2nd year (or the second term of the interest period) is more than the C.I. of Ist year (or the first term of the interest period), and C.I. of 2nd year -C.I. of Ist year = S.I. on the interest of the first year.
5. Equivalent, nominal and effective rates of interest
Two annual rates of interest with different conversion periods are called
equivalent if they yield the same compound amount at the end of the
year. For example, consider an amount of Rs 10,000 invested at 4% interest
compounded quarterly. So, the amount at the end of one year = 10000(1·01)4 =
10406. This is equivalent to interest of 4·06% compounded annually because
10000(1·0406) = 10406.
When interest is compounded more than once in a year, the given annual rate is
called nominal rate or nominal annual rate. The rate of interest
actually earned is called effective rate. In the above example, nominal rate
is 4% while effective rate is 4·06%.
If nominal rate is r% compounded p times in year, then effective rate of interest is
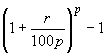
6. Present value or present worth of a sum of Rs P due n
years hence at r% compound interest is
P.V. = 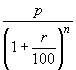
In particular, present value of sum of a Rs P due one year hence (i.e. n = 1)
at r% (compound) interest is
P.V.=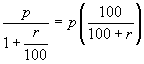
7. Equal instalments (with compound interest)
Loan amount = 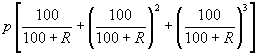 ,
where
,
where
P = each equal instalment
R = rate of interest per annum (or per interest period)
T = time, say 3 years (or 3 interest terms).
Note. If T = n years (or interest terms), then there will be n brackets.
8. Formulae for population
If the present population of a town is P and its annual increase is r%,
the population after n years will be P
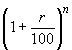 , and n years ago,
the population was
, and n years ago,
the population was 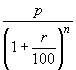 .
.
If, however, there is annual decrease of r% per annum, the population after n
years will be 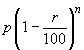 ,
and n years ago, the population was
,
and n years ago, the population was 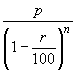 .
.
All fixed assets such as machinery, building, furniture etc. gradually
diminish in value as they get older and become worn out by constant use in
business. Depreciation is the term used to describe this
decrease in book value of an asset.
There are a number of methods of calculating depreciation. However, the most
common method which is also approved by income tax authorities, is the
Diminishing Balance Method. Here each years depreciation is calculated on
the book value (i.e., depreciated value) of the asset at the beginning of the
year rather than original cost. Note that as the book value decreases every
year, the amount of depreciation also decreases every year. Therefore, this
method is also called Reducing Instalment Method or "Written Down Value
Method".
If the rate of depreciation is i% per year and the initial value of the asset
is P, the depreciated value at the end of n years is
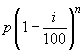 and the
amount of depreciation is
and the
amount of depreciation is
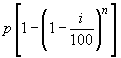 .
If n is large, log tables should be used for calculation.
.
If n is large, log tables should be used for calculation.
The number of years a machine can be effectively used is called its life span.
After that it is sold as waste or scrap.
Find the compound amount of Rs 1500 for 6 years 7 months, at 5·2% compounded semi annually.
Using formula, we could find the value of
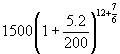
But in these kinds of problems, generally we use compound interest for full
interest period and simple interest for fractional interest period. Here we
find compound interest for 13 interest periods and simple interest for 1 month.
Required compound amount
A = 1500 ![]()
=1500(1·026)13(1·0043)
Taking logs,
log A = log 1500 +13 log (1·026) +log (1·0043)
= 3·1761
+13(0·0112) +0·0017) = 3·3234.
A = antilog (3·3234) = 2144
Thus the required compound amount is Rs 2144.
The simple interest in 3 years and the compound interest in 2 years on a certain sum at the same rate are Rs 1200 and Rs 832 respectively. Find (i) the rate of interest. (ii) the principal. (iii) the difference between the C.I. and S.I. for 3 years.
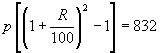
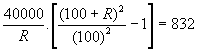
The population of an industrial town is increasing by 5% every year. If the present population is 1 million, estimate the population five years hence. Also estimate the population three years ago.
Present population, P = 1 million, rate of increase = 5% per annum
Hence population after 5 years =
![]()
= 1000000 ![]() =
1000000 (1·05)5
=
1000000 (1·05)5
= 1276280
Population three years ago =
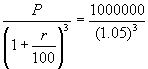 = 863838.
= 863838.
Avichal Publishers buy a machine for Rs 20000. The rate of depreciation is 10%. Find the depreciated value of the machine after 3 years. Also find the amount of depreciation. What is the average rate of depreciation?
Original value of machine = Rs 20000,
Rate of depreciation, i = 10%
Hence the book value after 3 years = 20000
![]()
= 20000 (0·9)³ = 20000 (0·729) = Rs 14580.
Amount of depreciation in 3 years = Rs 20000 -Rs 14580 = Rs 5420
Average rate of depreciation in 3 years
= (5420/20000) x (100/3) = 9·033%
1. (i) Rs 784 (ii) Rs 6384
(iii) Rs 894
2. Rs 13240
3. 4% p.a.; Rs 1875
4. Rs 20000
5. Rs 1275
6. Rs 17640
7. Rs 1464·10
8. Rs 1177
9. Rs 3679·50
10. Rs 11466 and Rs 10400
11. Rs 5565, Rs 4435
[Hint. x (1·12)³ = (10000 - x) (1·12)5]
12. He should accept (b)
13. Rs 15496
14. Rs 166636·50
15. Rs 8748
16. Rs 137200
17. Rs 65664·50, Rs 47869·40
18. Rs 85 lacs approx.
19. Rs 33438
20. 5 years
21. 5·926%, 6·09%
22. Rs 20000; Rs 16928