Orthogonal Circles

Angle of intersection of two circles

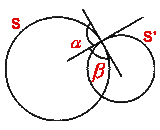
An angle between the two tangents to the two circles at a point of intersection is called an angle of intersection between two circles.

Orthogonal circles

Two circles are said to cut orthogonally iff angle of intersection of these circles at a point of intersection is a right angle i.e. iff the tangents to these circles at a common point are perpendicular to each other.

If r, r' are radii of circles S and S' respectively and d is the distance between their centers and is an angle of intersection of these circles, then
               cos =(r² +r'² -d²)/(2 r r')

If the circles S and S' cut orthogonally, then = 90°,cos = cos 90° = 0
    => (r² +r'² -d²)/(2r r') = 0
    => r² +r'² = d²

Two circles S = x² +y² +2gx +2 f y +c = 0 and
S' = x² +y² +2 g' x +2 f'y +c' = 0 cut orthogonally if 2 (g g' +f f') = c +c'.

Illustrative Examples

Example

Find the equation of the circle which intersects the circles x² +y² +2 x -2 y +1 = 0 and x² +y² +4 x -4 y +3 = 0 orthogonally and whose center lies on the line 3 x -y -2 = 0.

Solution

Let the equation of the required circle be
     x² +y² +2 g x +2 f y + c = 0 ...(i)
Since this circle cuts the circles x² +y² +2 x -2 y +1 = 0 and x² + y² +4 x -4 y +3 = 0 orthogonally, we get
       2 (g. 1 + f. (-1)) = c +1
=>   2 g -2 f - c -1 = 0              ...(ii)
and 2 (g.2 + f.(-2)) = c +3
=>   4 g -4 f -c -3 = 0               ...(iii)
As center of (i) i.e. (-g, -f) lies on 3 x -y -2 = 0, we get
     -3 g + f -2 = 0
=>    3 g - f +2 = 0                   ...(iv)
Subtracting (ii) from (iii), we get
       2 g -2 f -2 = 0
=>  g -f -1 = 0                            ...(v)
Solving (iv) and (v) simultaneously, we get g = -3/2 and f = -5/2
From (ii), we get c = 2 g -2 f -1 = -3 +5 -1 = 1
Substituting these values of g, f and c in (i), we get
x² +y² -3 x -5 y +1 = 0, which is the equation of the required circle.

Exercise

1. Determine the angle of intersection of the two circles (x -3)² +(y -1)² = 8 and (x -2)² +(y +2)² = 2.
2. Find the angle at which the circles x² + y² = 16 and x² +y² -2 x -4 y = 0 intersect each other.
3. Show that the circles x² + y² -4 x  -6 y +4 = 0 and x² +y² -10 x -14 y +58 = 0 cut orthogonally.
4. Show that the circles x² +y² -2 a x +2 b y + c = 0 and x² + y² +2 bx +2 a y -c = 0, a² + b² > | c |, cut orthogonally.
5. For what value of  do the circles x² + y² +5 x +3 y +7 = 0 and x² +y² -8 x +6 y + = 0 cut orthogonally?

Answers